Naughty Nathan Junk from the mind of a Tech Artist…

Labyrinth is a new puzzle I recently discovered that takes the logic of Picross/Hanjie and adds a new dimension. Here’s a very simple 6×6 sample:

Each labyrinth puzzle consists of an empty board with a series of numbers along the left and top edges and a Start(S) and End(E) point marked (as seen above). The goal is to fill in a complete labyrinth of walls, tracing a continuous path from Start to End, visiting every square on the board grid once and once only.

As mentioned before, solutions are derived using the same logic rules as Picross (trad. known as Hanjie) so if you’ve played either of those games before, labyrinth should be very easy to pick up.

Walls and path may only be drawn horizontally and vertically, the walls are drawn along the grid lines and the path is drawn from square to square (center to center).

The numbers given along each edge denote how many wall sections there are on that grid line, and how long each section is. For example:

means that along this particular horizontal grid line there are four separate sections of wall. The first wall is 2 grid units long, followed by a wall a single unit long, followed by a wall 3 grid units long and finally another wall 1 unit long. There must be at least one segment gap between each section of wall and the sections are always drawn in the order shown (i.e. 2 first (leftmost), then 1, followed by the 3, and finally (rightmost) a 1). Because the grid in this example line is only 10 units wide, there is only one possible solution:

and once we know where there is no wall we can mark the path in:

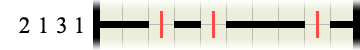
However, you will not always immediately know where all the wall segments go, for example the following line is not so conclusive:

Still, no matter where the 6-length wall actually is on this line we can be sure that the two central spaces must be occupied by it, so we can mark those in right away:

the remaining four sections of this wall will have to be deduced later by some other method but, for arguments sake, lets assume that sometime later on we are able to add a path line here:

we can now safely deduce that the first two squares must also be paths (otherwise we’d have TWO wall sections, one of 2 and one of unknown length, and our edge numbers for this line clearly show there is only a single wall of length 6). It is obvious now that the wall has to start from at least the fourth grid section, so we know it must run up to at least the ninth, as it’s 6 long. We’re only 1 square off completing this line now:

As you can see this is typical Picross/Hanjie logic.

Once we have one full section of wall in we can draw some of the path in. For example if we somehow end up with this:

It will immediately give us:

and then, because we can see that the only other wall on this row is on the right of the 4 wall we know that there can’t be another wall in the first square, so it must also contain a path:

the 1-long wall must be in one of the remaining 3 grid spaces.

We can see that drawing the walls helps us to determine the path, and drawing the path helps us to determine where the walls are.

Common Tips:

The path always starts from S and terminates at E and must visit every square on the grid once and only once. This is a key factor in solving every labyrinth puzzle as in certain common situations it helps dictate where a wall or path can or cannot be. For example, in any labyrinth there cannot be any T-junctions, crossroads or dead-ends (except S and E which have to be dead-ends!), therefore, in any situation where adding a wall would cause a dead-end you know it must be a pathway.

Corners – One situation where this crops up the most is in corners. Wherever and whenever you find an inside corner you can always draw the path straight away (unless it has a S or E in it!). Take the following scenario for example:

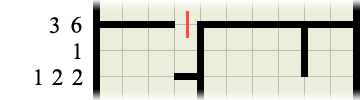
Without even bothering to check or consider where any other walls or path may be we can immediately fill in the paths inside each and every corner as so:

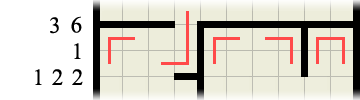
This then immediately provides us with another wall clue:

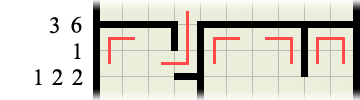
which in turn gives us another corner to fill the path in at…

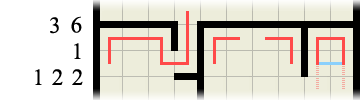
Finally, if you consider the right-hand portion of the labyrinth in the above image, we can deduce that the path CANNOT run horizontally (highlighted in blue) as this would produce an invalid path loop. Therefore there must be a wall there, which in turn means the path must run downwards (highlighted in faint pink)

0 (zero) walls – If the wall sections number is 0, meaning there are no wall segments along this line you can immediately draw paths between every set of squares along this grid line:

This is also true whenever you have filled in all the given wall segments on a line:

means you can fill in the rest like so:

S and E side by side – If the S and E are ever alongside one another you can immediately draw a wall between the two as so:

Vertical grid lines follow exactly the same principles as all the examples above, except vertically! 😉

There should only ever be one possible unique solution per puzzle and no guessing is required.

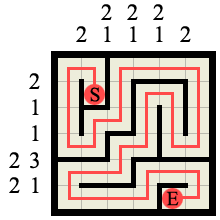
Here’s a sample solution (to the example 6×6 labyrinth shown at the start). Notice how the path is a single continuous line from S to E and it visits every square on the board without splitting or crossing itself.

Finally, here’s a couple of easy 8×8 puzzle to try (dump them into photoshop or print them out)

---

---

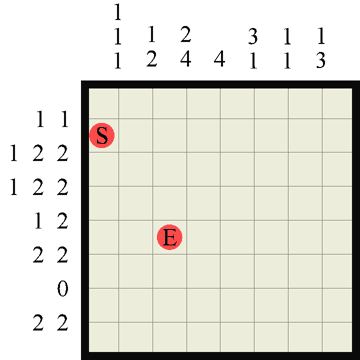
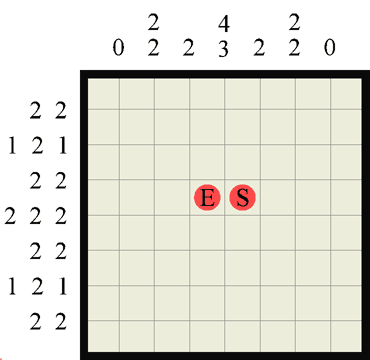
I’ll be adding more puzzles frequently, and shortly a Maya python script to play them dynamically in 3D!!
Have Fun!